【数据结构】利用栈实现正整数四则运算
Published:
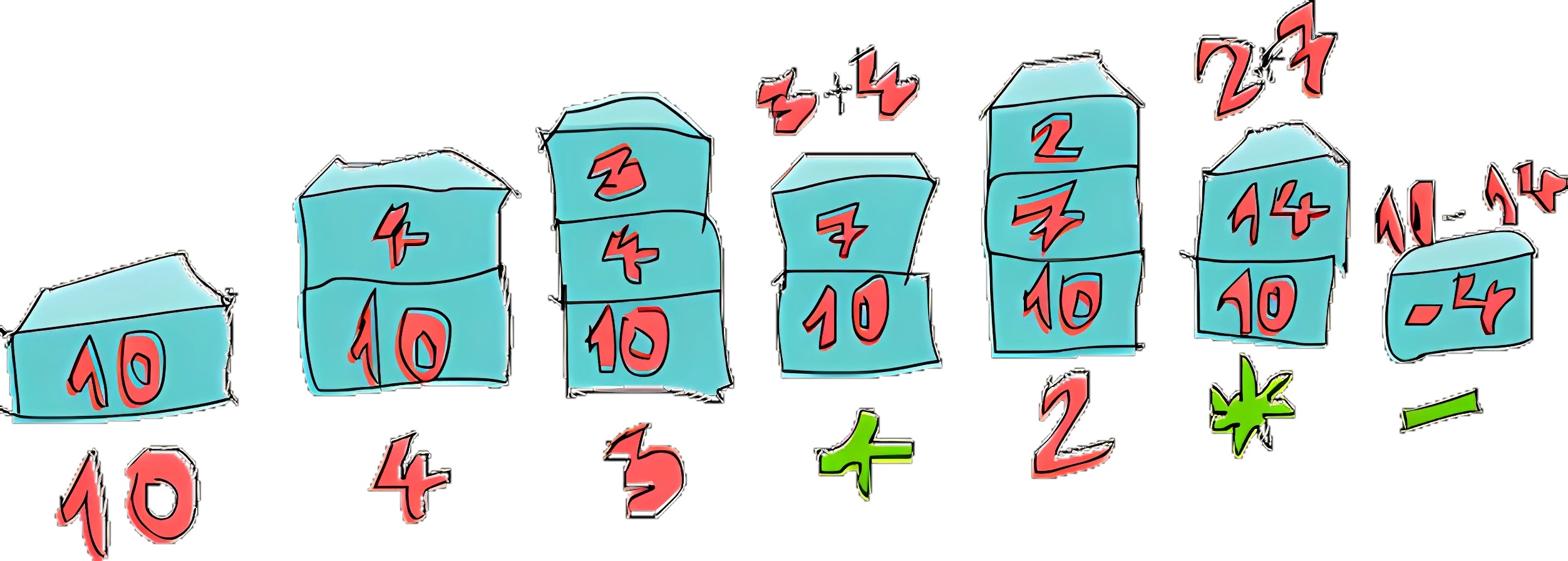
栈的基本知识
首先,什么是栈。
栈是一种线性的数据结构,只允许在一端进行数据的插入和删除。简单来说,栈是用来存储数据的,有头(栈底)有尾(栈顶),但是只允许从栈顶取出数据(出栈),或者把数据放到栈顶(入栈)。下面这幅图中,用蓝色长方形表示栈中存储的数据,最底部是栈底,最上部是栈顶。你只能把数据(蓝色长方形)从上面拿走(pop),或者从最上面添加新的数据(push)。即后入栈的元素可以先出栈(Last in First out – LIFO)。

在 C++ 中,有封装好的栈类:stack,支持数据的存取。
// 头文件
#include <stack>
// 栈的初始化
stack<int> stack;
// 入栈
stack.push(21);
// 出栈
stack.pop();
// 检查栈是否为空
stack.empty()
// 获取栈顶元素
int elem = stack.top();
在 Python 中,list 支持栈的各种操作。
# 创造一个空栈
stack = []
# 入栈
stack.append(3)
# 出栈
elem = stack.pop()
# 检查栈是否为空(栈中元素个数是否为0)
len(stack) > 0
# 获取栈顶元素
elem = stack[-1]
逆波兰表示
基础知识介绍完了,进入正题:如何编写一个程序来进行四则运算呢?
我们看到 12 +(3 + 4)\(\times\) 5 / 7 可以很快就算出来答案是 17,因为我们知道要先计算括号里面的加法,然后先乘除,后加减,最后得到计算结果。可是对计算机程序来说,输入是一个字符串,需要区分数字、运算符、括号,然后需要按照前面的运算顺序执行,才能得到结果。
为了更好地编程实现四则元算,我们要引入一个新的算数表示法——逆波兰表示,之所以叫这个名,是因为它的发明者是一位波兰的数学家。在逆波兰表示中,操作符( +,-,\(\times\),/)是位于操作数后面的,而不是位于中间。举个简单的例子,3 + 4 的逆波兰表示就是 3 4 +。12 +(3 + 4)\(\times\) 5 / 7 的逆波兰表示是 12 3 4 + 5 7 / \(\times\) +。
逆波兰表示转化的算法及代码
如何把我们熟悉的四则运算表达式转化为逆波兰表示呢?
还是要利用栈的后进先出特性。下面简要描述将常规四则元算表达式转化为逆波兰表示的步骤:
创建一个空栈。
从左至右遍历常规四则元算表达式的字符,对每一个字符:
1. 若字符是数字,则将其添加到输出的表达式的尾端;
2. 若字符是左括号 "(",则将其入栈;
3. 若字符是 "+" 或者 "-",则把栈中元素依次出栈,添加到输出表达式的末尾,直到栈顶元素是左括号 "(" ,
或者栈变为空栈,再把字符入栈;
4. 若字符是 "$$\times$$" 或者 "/",则将其入栈;
5. 若字符是有括号 ")",则把栈中元素依次出栈,添加到输出表达式末尾,直到栈顶元素是是左括号 "(",然后将左括号出栈。
遍历玩所有字符以后,如果栈非空,则将栈中元素依次出栈,添加到输出表达式末尾。
下图显示了将 12 +(3 + 4)\(\times\) 5 / 7 转化为逆波兰表示过程中,栈中元素以及输出表达式的变化。
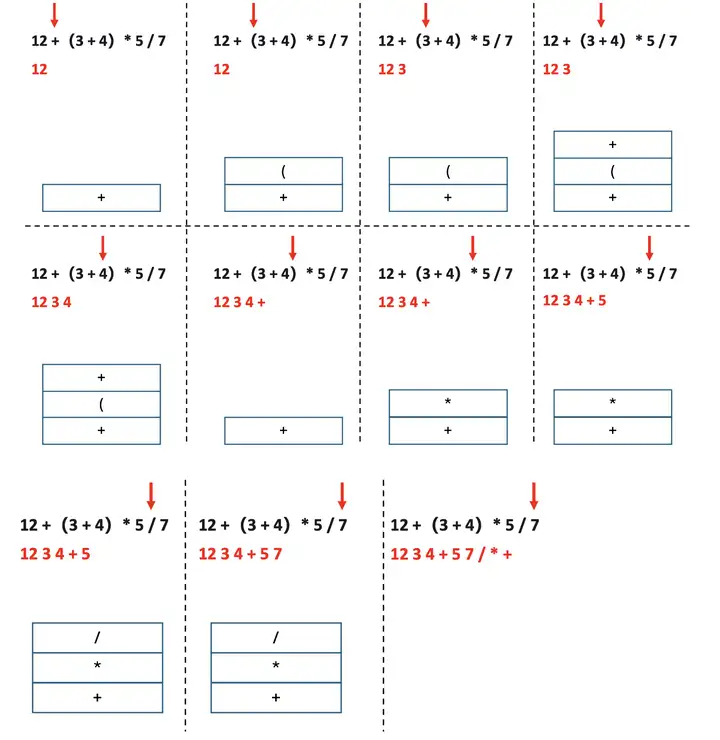
下面是将输入常规四则运算表达式变为逆波兰表示的 Python 代码。
in_expression = "12+(3+4)*5/7"
stack = []
out_expression = ""
for c in in_expression:
if c == " ":
continue
if c == "(":
stack.append(c)
elif c == "+" or c == "-":
out_expression += " "
if len(stack) == 0:
stack.append(c)
else:
while len(stack) > 0 and stack[-1]!= "(":
out_expression += stack.pop()
stack.append(c)
elif c == "*" or c == "/":
out_expression += " "
stack.append(c)
elif c == ")":
out_expression += " "
while len(stack) > 0 and stack[-1] != "(":
out_expression += stack.pop()
if len(stack) > 0:
stack.pop()
else:
out_expression += c
while len(stack) > 0:
out_expression += stack.pop()
print("in expression :" + in_expression)
print("out expression :" + out_expression)
逆波兰表达式求值
有了逆波兰表达式,求值就变的很方便了。还是需要利用栈后进先出的特性。下面是对逆波兰表示的求值步骤:
创建一个空栈。
从左至右遍历逆波兰表达式:
1. 若当前元素为数值,则入栈;
2. 若当前元素为运算符,则将栈顶两个元素出栈,以它们作为操作数,当前元素为操作符,进行运算,将运算结果入栈。
当遍历完成时,栈顶元素出栈,即为最终运算结果。
注意,在逆波兰表示中,连续的数字需要用一定的标记符号来隔开,在这里,我用的是空格符号。在上面的算法中,没有提到这一点,但是在写代码的时候,需要注意。
下面是遍历逆波兰表达式 12 3 4 + 5 7 / \(\times\) + 求值的过程。 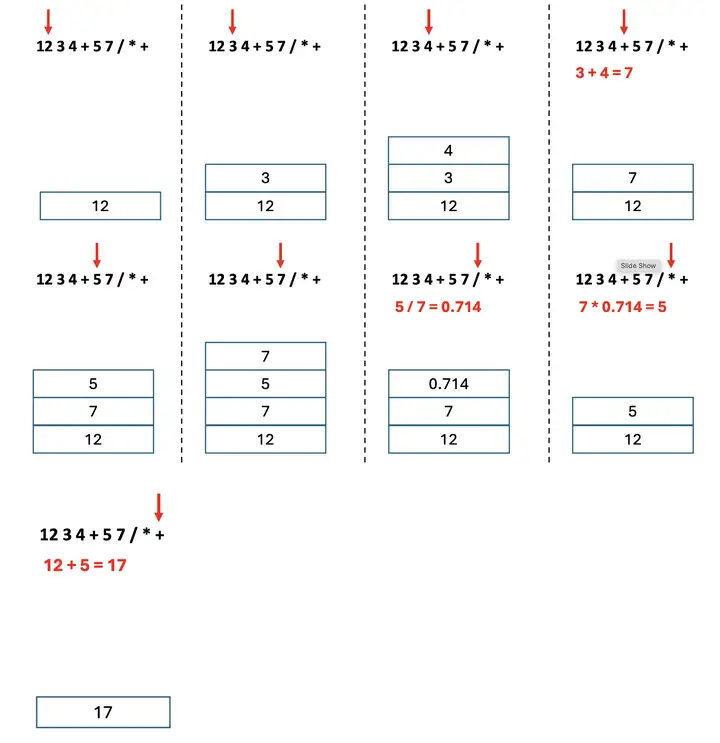
下面是利用逆波兰表达式求值的 Python 代码。
out_expression = "12 3 4 + 5 7/*+"
stack = []
i = 0
while i < len(out_expression):
if out_expression[i] in ['0', '1', '2', '3', '4', '5', '6', '7', '8', '9']:
j = i + 1
while j < len(out_expression) and out_expression[j] in ['0', '1', '2', '3', '4', '5', '6', '7', '8', '9']:
j += 1
stack.append(int(out_expression[i:j]))
i = j
continue
elif out_expression[i] == '+':
num2 = stack.pop()
num1 = stack.pop()
stack.append(num1 + num2)
elif out_expression[i] == '-':
num2 = stack.pop()
num1 = stack.pop()
stack.append(num1 - num2)
elif out_expression[i] == '*':
num2 = stack.pop()
num1 = stack.pop()
stack.append(num1 * num2)
elif out_expression[i] == '/':
num2 = stack.pop()
num1 = stack.pop()
stack.append(num1 / num2)
i += 1
print(stack[-1])