Harris角点检测Python实现
Published:

图像处理作业,分享出来。不足之处,多多见谅。欢迎提出改进意见。
原理
所谓角点,即为边的交点。在图像中,创建一个包含角点的局部窗口,那么将该窗口按照任意方向滑动,窗口内的像素平均值都会发生比较大的变化。如果窗口在像素变化平缓的区域内滑动,窗口内的像素平均值不会显著变化;如果窗口在包含边的区域内滑动,沿着边的方向滑动,窗口内的像素平均值不会显著变化,而沿着垂直于边的方向滑动,窗口内的像素平均值会发生较大的变化。 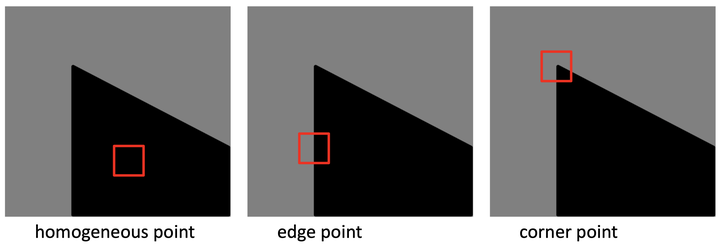
所以,对于图像中的某个点,我们需要一个函数,来衡量包含该点的窗口内的像素平均值对滑动的敏感度。对于窗口\(W\)和位移\(\Delta\),定义窗口函数\(S_{W}\)。该函数计算窗口沿着某个方向移动后,窗口内的每个点的像素变化值的平方和。
\[\Delta = [\Delta x, \Delta y]\] \[S_{W}(\Delta) = \sum_{(x_i, y_i) \in W}^{}{(f(x_i, y_i) - f(x_i + \Delta x, y_i + \Delta y))}^{2}\]用泰勒展开公式,可以得到
\[f(x_i + \Delta x, y_i + \Delta y) \approx f(x_i, y_i) + \begin{bmatrix} \frac{\partial f(x_i, y_i)}{\partial x} & \frac{\partial f(x_i, y_i)}{\partial y} \end{bmatrix} \begin{bmatrix} \Delta x \\ \Delta y \end{bmatrix}\] \[S_W(\Delta) = \sum_{(x_i,y_i)\in W} [\Delta x, \Delta y] \left[ \begin{array}{cc} \left(\frac{\partial f(x_i,y_i)}{\partial x}\right)^2 & \frac{\partial f(x_i,y_i)}{\partial x} \frac{\partial f(x_i,y_i)}{\partial y} \\ \frac{\partial f(x_i,y_i)}{\partial x} \frac{\partial f(x_i,y_i)}{\partial y} & \left(\frac{\partial f(x_i,y_i)}{\partial y}\right)^2 \end{array} \right] [\Delta x, \Delta y]^T\] \[S_W(\Delta) = [\Delta x, \Delta y] \left[ \begin{array}{cc} \sum_{(x_i,y_i)\in W} \left(\frac{\partial f(x_i,y_i)}{\partial x}\right)^2 & \sum_{(x_i,y_i)\in W} \frac{\partial f(x_i,y_i)}{\partial x} \frac{\partial f(x_i,y_i)}{\partial y} \\ \sum_{(x_i,y_i)\in W} \frac{\partial f(x_i,y_i)}{\partial x} \frac{\partial f(x_i,y_i)}{\partial y} & \sum_{(x_i,y_i)\in W} \left(\frac{\partial f(x_i,y_i)}{\partial y}\right)^2 \end{array} \right] [\Delta x, \Delta y]^T\] \[S_W(\Delta) = [\Delta x, \Delta y] A_W (x, y) [\Delta x, \Delta y]^T\]矩阵\(A_W(x, y)\)被称为 Harris 矩阵,它是一个对称矩阵,也是一个半正定矩阵。所以,可以求解该矩阵的特征值和特征向量。这两个特征值\((\lambda_1 , \lambda_2)\)可以体现窗口\(W\)内图像梯度沿着特征向量的变化幅度。基于\((\lambda_1 , \lambda_2)\)的取值,可以将窗口\(W\)包含区域分为三种情形。
- \(\lambda_1\)和\(\lambda_2\)都很小:没有边或者角点,窗口\(W\)所包围的是一个像素均匀分布和缓慢变化的区域。
- \(\lambda_1\)和\(\lambda_2\)都很小:窗口\(W\)所包围的区域存在边,没有角点。
- \(\lambda_1\)和\(\lambda_2\)都很小:窗口\(W\)所包围的区域存在角点。
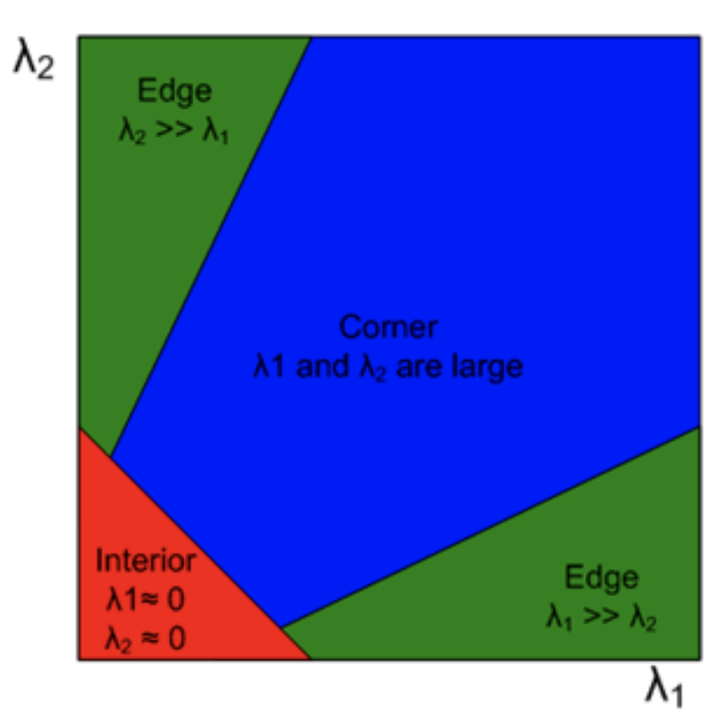
为了更方便地找到角点,定义函数\(R(A_W)\)如下,其中\(\kappa\)的取值范围是 0.04 和 0.10 之间。 \(R(A_W) = det (A_W) - \kappa {(trace(A_W))}^{2} = (\lambda_1 \times \lambda_2) - \kappa {(\lambda_1 + \lambda_2)}^{2}\)
设定适当的阈值,若\(R(A_W)\)高于该阈值,则该区域包含角点。
处理流程及代码实现
第一步,读取图片,将图片转化为单通道的灰度图,然后对其进行高斯模糊。下面是图片处理结果以及代码。除了定义了高斯模糊的函数,还定义了一个对图片的边缘进行像素补充的函数。 
## Read image and convert to grayscale image
import cv2
import matplotlib.pyplot as plt
import numpy as np
img_path = '/path/to/image/file'
img_rgb = cv2.imread(img_path)
img_gray = cv2.cvtColor(img_rgb, cv2.COLOR_BGR2GRAY)
img_gray = img_gray.astype(np.float32)
## generate padding image with padding size, padding mode "mirror"
def padding_img(img, padding_size):
padding_topleft = img[0: padding_size, 0: padding_size]; padding_topleft = np.flip(padding_topleft, 0); padding_topleft = np.flip(padding_topleft, 1)
padding_topright = img[0: padding_size, img.shape[1] - padding_size: img.shape[1]]; padding_topright = np.flip(padding_topright, 0); padding_topright = np.flip(padding_topright, 1)
padding_bottomleft = img[img.shape[0] - padding_size: img.shape[0], 0: padding_size]; padding_bottomleft = np.flip(padding_bottomleft, 0); padding_bottomleft = np.flip(padding_bottomleft, 1)
padding_bottomright = img[img.shape[0] - padding_size: img.shape[0], img.shape[1] - padding_size: img.shape[1]]; padding_bottomright = np.flip(padding_bottomright, 0); padding_bottomright = np.flip(padding_bottomright, 1)
padding_top = img[0: padding_size, :]; padding_top = np.flip(padding_top, 0)
padding_bottom = img[img.shape[0] - padding_size: img.shape[0], :]; padding_bottom = np.flip(padding_bottom, 0)
padding_left = img[:, 0: padding_size]; padding_left = np.flip(padding_left, 1)
padding_right = img[:, img.shape[1] - padding_size:img.shape[1]]; padding_right = np.flip(padding_right, 1)
img_padding = np.block([[padding_topleft, padding_top, padding_topright],
[padding_left, img, padding_right],
[padding_bottomleft, padding_bottom, padding_bottomright]])
return img_padding
## apply gaussian filter to the input image
def gaussian_filtering(img, sigma = 1, muu = 0, kernel_size = 3):
# generate gaussian filter kernel
x, y = np.meshgrid(np.linspace(-2, 2, kernel_size),
np.linspace(-2, 2, kernel_size))
dst = np.sqrt(x**2 + y**2)
normal = 1/(2 * np.pi * sigma**2)
gauss = np.exp(-((dst - muu)**2 / (2.0 * sigma**2))) * normal
padding_size = int(kernel_size/2)
img_padding = padding_img(img, padding_size)
img_filtered = np.zeros_like(img)
for i in range(img.shape[0]):
for j in range(img.shape[1]):
img_filtered[i][j] = np.sum(np.multiply(img_padding[i: i + kernel_size, j: j + kernel_size], gauss))
return img_filtered
img_filtered = gaussian_filtering(img_gray, kernel_size = 3)
第二步,用 Sobel 算子计算图像的水平和垂直方向的梯度。下面是图像处理结果以及代码。 
# calculate gradient with sobel operator
def sobel_operator(img):
sobel_x = 1/8 * np.array([[-1, 0, 1], [-2, 0, 2], [-1, 0, 1]])
sobel_y = 1/8 * np.array([[-1, -2, -1], [0, 0, 0], [1, 2, 1]])
padding_size = 1
img_padding = padding_img(img, padding_size)
img_h_gradient = np.zeros_like(img)
img_v_gradient = np.zeros_like(img)
for i in range(img.shape[0]):
for j in range(img.shape[1]):
img_h_gradient[i][j] = np.sum(np.multiply(img_padding[i: i + 3, j: j + 3], sobel_x))
img_v_gradient[i][j] = np.sum(np.multiply(img_padding[i: i + 3, j: j + 3], sobel_y))
# dx = cv2.Sobel(img, cv2.CV_64F, 1, 0, ksize=3)
# dy = cv2.Sobel(img, cv2.CV_64F, 0, 1, ksize=3)
return (img_h_gradient, img_v_gradient)
(img_h_gradient, img_v_gradient) = sobel_operator(img_filtered)
第三步,对于图像中的每个像素,计算Harris矩阵\(\)和函数值\(\),选定合适的阈值,保留包含角点的区域。下面是处理后的图像和代码。 
## Calculate Harris Matrix and Response function
def calculate_harris_response(img_h_gradient, img_v_gradient, k, window_size = 3):
response_matrix = np.zeros_like(img_h_gradient)
padding_size = int(window_size/2)
img_h_gradient_padding = padding_img(img_h_gradient, padding_size)
img_v_gradient_padding = padding_img(img_v_gradient, padding_size)
for i in range(response_matrix.shape[0]):
for j in range(response_matrix.shape[1]):
matrix_a = np.array([[np.sum(np.multiply(img_h_gradient_padding[i: i + window_size, j: j + window_size], img_h_gradient_padding[i: i + window_size, j: j + window_size])),
np.sum(np.multiply(img_h_gradient_padding[i: i + window_size, j: j + window_size], img_v_gradient_padding[i: i + window_size, j: j + window_size]))],
[np.sum(np.multiply(img_h_gradient_padding[i: i + window_size, j: j + window_size], img_v_gradient_padding[i: i + window_size, j: j + window_size])),
np.sum(np.multiply(img_v_gradient_padding[i: i + window_size, j: j + window_size], img_v_gradient_padding[i: i + window_size, j: j + window_size]))]])
response_matrix[i][j] = np.linalg.det(matrix_a) - k * (np.matrix.trace(matrix_a)**2)
return response_matrix
response_matrix = calculate_harris_response(img_h_gradient, img_v_gradient, 0.04)
cv2.normalize(response_matrix, response_matrix, 0, 1, cv2.NORM_MINMAX)
response_thresh = 0.5
response_matrix_thres = np.copy(response_matrix)
response_matrix_thres[response_matrix_thres < response_thresh] = 0
第四步,对所得的角点区域进行非极大值抑制处理。简单地说,我们在上一步会得到一系列孤立的区域,如图五中的白点所示,我们需要进一步把每个白点区域中的极大值点找到,将该点作为最终角点。下面是图像处理结果以及代码。 
## Non-maximal suppression to get the final corner pixels
## Divide the input response matirx map into grids, find
# the local maximal pixel for each grid, add it to the corner list
def localmax_loc(response_patch, threshold, offset):
max_pixel = np.max(response_patch)
if max_pixel > threshold:
max_ind = np.where(response_patch == max_pixel)
max_ind = list(max_ind)
for i in range(len(max_ind)):
max_ind[i] = max_ind[i] + offset
return max_ind
else:
return None
def nms_corners(response_matrix, window_size = 7):
grid_size = [int(response_matrix.shape[0]/window_size), int(response_matrix.shape[1]/window_size)]
corner_ind = []
for i in range(grid_size[0] + 1):
for j in range(grid_size[1] + 1):
loc = localmax_loc(response_matrix[i*window_size: (i + 1)*window_size, j*window_size: (j + 1)*window_size],
0.2, np.array([i*window_size, j*window_size]))
if loc is not None:
corner_ind.append(loc[0])
return corner_ind
# from itertools import chain
corner_ind = nms_corners(response_matrix_thres)
print(f'{len(corner_ind)} corners detected')
img_path = '/path/to/image'
img_rgb = cv2.imread(img_path)
img_corner = np.copy(img_rgb)
for corner in corner_ind:
cv2.circle(img_corner,(corner[1],corner[0]),2,(0,255,0))